Hàm lượng giác là các hàm toán học của góc, được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất tuần hoàn. Các hàm lượng giác của một góc thường được định nghĩa bởi tỷ lệ chiều dài hai cạnh của tam giác vuông chứa góc đó, hoặc tỷ lệ chiều dài giữa các đoạn thẳng nối các điểm đặc biệt trên vòng tròn đơn vị.
Những định nghĩa hiện đại hơn thường coi các hàm lượng giác là chuỗi số vô hạn hoặc là nghiệm của một số phương trình vi phân, điều này cho phép hàm lượng giác có thể có đối số là một số thực hay một số phức bất kì.
=> Các hàm lượng giác không phải là các hàm số đại số và có thể xếp vào loại hàm số siêu việt.
=> Bạn có thể xem thêm các công thức lượng giác ở đây bài viết của THPT Chuyên Lam Sơn chi tiết : https://thptchuyenlamson.vn/cong-thuc-luong-giac/
Định nghĩa hàm lượng giác bằng tam giác vuông
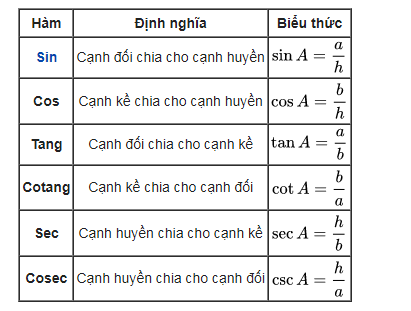
Có thể định nghĩa các hàm lượng giác của góc A, bằng việc dựng nên một tam giác vuông chứa góc A. Trong tam giác vuông này, các cạnh được đặt tên như sau:
- Cạnh huyền là cạnh đối diện với góc vuông, là cạnh dài nhất của tam giác vuông, h trên hình vẽ.
- Cạnh đối là cạnh đối diện với góc A, a trên hình vẽ.
- Cạnh kề là cạnh nối giữa góc A và góc vuông, b trên hình vẽ.
Dùng hình học Ơclit, tổng các góc trong tam giác là pi radian (hay 180⁰). Khi đó:
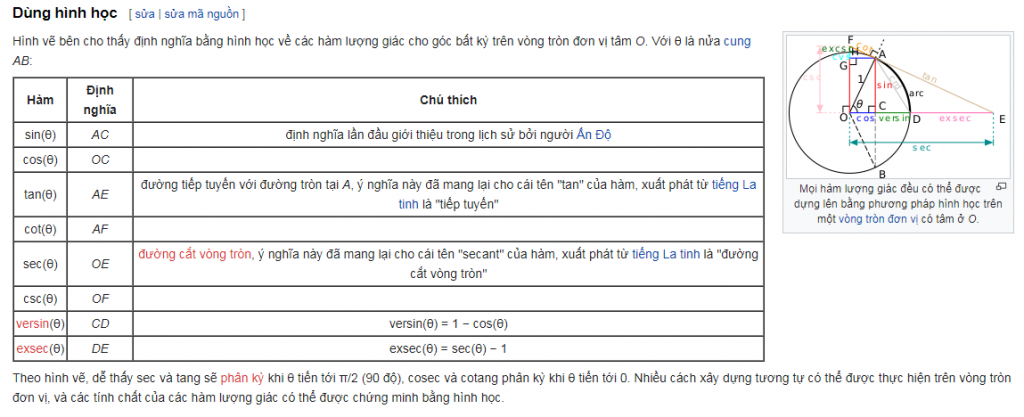
Định nghĩa hàm lượng giác bằng vòng tròn đơn vị
Các hàm lượng giác cũng có thể được định nghĩa bằng vòng tròn đơn vị, một vòng tròn có bán kính bằng 1 và tâm trùng với tâm của hệ tọa độ.
Định nghĩa dùng vòng tròn đơn vị thực ra cũng dựa vào tam giác vuông, nhưng chúng có thể định nghĩa cho các mọi góc là số thực, chứ không chỉ giới hạn giữa 0 và Pi/2 radian. Các góc lớn hơn 2π hay nhỏ hơn −2π quay vòng trên đường tròn.
Định nghĩa hàm lượng giác bằng chuỗi
Dùng hình học và các tính chất của giới hạn hàm số, có thể chứng minh rằng đạo hàm của hàm sin là hàm cos và đạo hàm của hàm cos là trái dấu của hàm sin. Có thể dùng chuỗi Taylor để phân tích hàm sin và cos ra chuỗi, cho mọi góc x đo bằng giá trị radian thực. Từ hai hàm này có thể suy ra chuỗi của các hàm lượng dạng còn lại.
Các đẳng thức bên dưới đây cho biết chuỗi Taylor của các hàm lượng giác. Chúng có thể dùng làm định nghĩa cho hàm lượng giác. Chúng được dùng trong nhiều ứng dụng, như chuỗi Fourier), vì lý thuyết của chuỗi vô hạn có thể được xây dựng từ nền tảng hệ thống số thực, độc lập với hình học. Các tính chất như khả vi hay liên tục có thể được chứng minh chỉ từ định nghĩa bằng chuỗi.
Trong bảng dưới, quy ước:
- En là số Euler thứ n
- Un là số lên/xuống thứ n
Thông qua bài viết của chúng tôi mong bạn sẽ hiểu hơn về hàm lượng giác, định nghĩa của hàm lượng giác trên các phương diện khác nhau.
- Nguồn tham khảo Wikipedia